Joints Framework in Physics/Mechanics

sympy.physics.mechanics provides a joints framework. This system consists of two parts. The first are the joints themselves, which are used to create connections between bodies. The second part is the JointsMethod, which is used to form the equations of motion. Both of these parts are doing what we can call “book-keeping”: keeping track of the relationships between bodies.

Joints in Physics/Mechanics

The general task of the joints is creating kinematic relationships between bodies. Each joint has a setup as shown in the image below (this is the example of the PrismaticJoint).

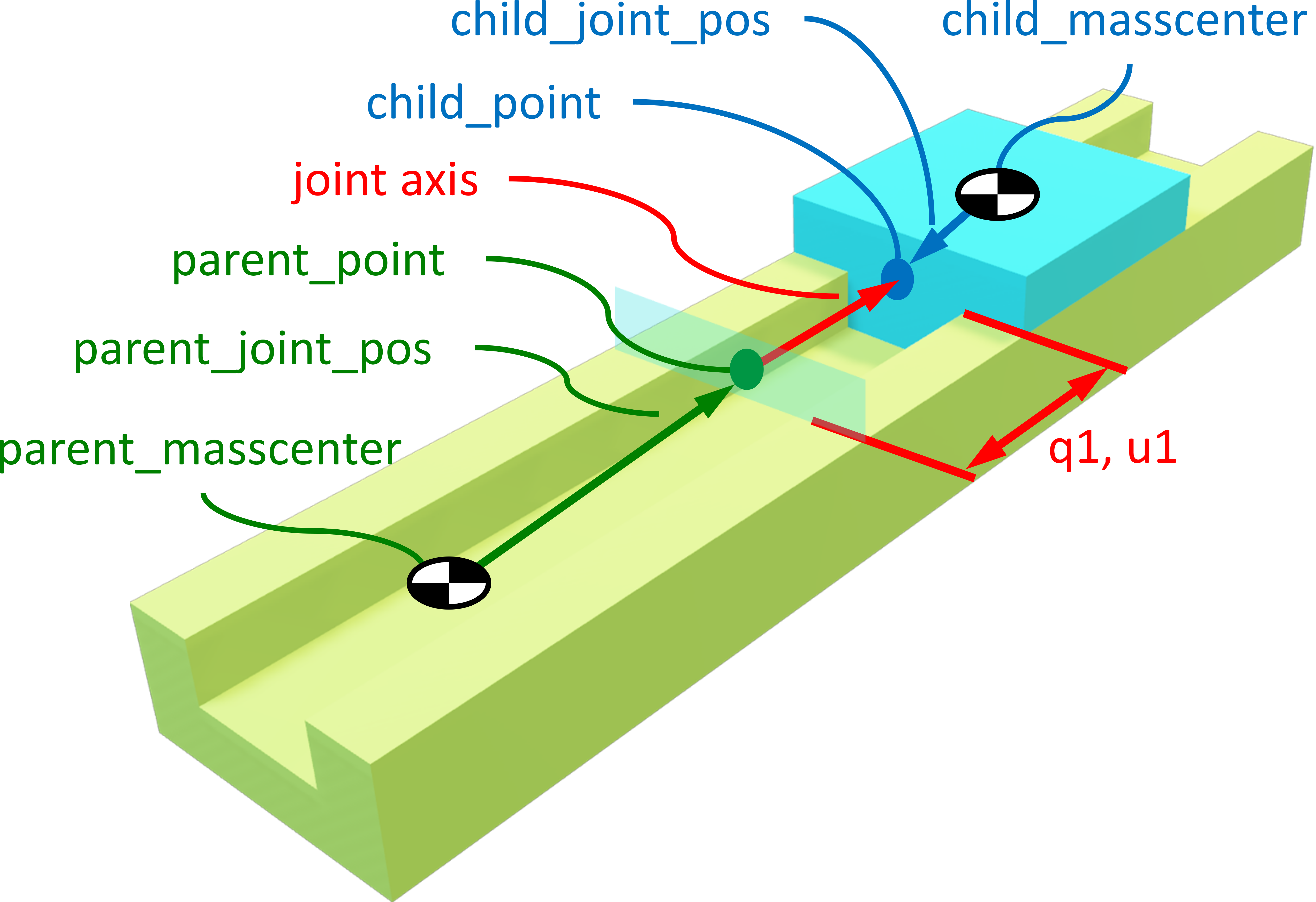
As can be seen in this image, each joint needs several objects in order to define the relationships. First off it needs two bodies: the parent body (shown in green) and the child body (shown in blue). Both of these bodies have a mass center from which the position of the joint is defined. In the parent body the vector from the mass center to the parent_point is called the parent_joint_pos. For the child body these are called the child_point and child_joint_pos. The orientation of the joint in each body is defined by the parent_axis and child_axis. These two vectors are aligned as explained in the Joint notes and are in the image parallel to the red vector. As last the joint also needs dynamicsymbols() as generalized coordinates and speeds. In the case of the PrismaticJoint shown above, the generalized coordinate q_1 distance along the joint axis. And the generalized speed u_1 is its velocity.

With the information listed above, the joint defines the following relationships. It first defines the kinematic differential equations, which relate the generalized coordinates to the generalized speeds. Next, it orients the parent and child body with respect to each other. After which it also defines their velocity relationships.

The following code shows the creation of a PrismaticJoint as shown above with arbitrary linked position vectors:

>>> from sympy.physics.mechanics import *
>>> mechanics_printing(pretty_print=False)
>>> q1, u1 = dynamicsymbols('q1, u1')
>>> parent = Body('parent')
>>> child = Body('child')
>>> joint = PrismaticJoint(
...     'slider', parent, child, q1, u1,
...     parent_joint_pos=parent.frame.x / 2 + parent.frame.y / 10,
...     child_joint_pos=-(child.frame.x + child.frame.y) / 10,
...     parent_axis=parent.frame.x, child_axis=child.frame.x)
>>> joint.kdes
[u1 - q1']
>>> child.masscenter.pos_from(parent.masscenter)
(q1 + 1/2)*parent_frame.x + 1/10*parent_frame.y + 1/10*child_frame.x + 1/10*child_frame.y
>>> child.masscenter.vel(parent.frame)
u1*parent_frame.x

JointsMethod in Physics/Mechanics

After defining the entire system you can use the JointsMethod to parse the system and form the equations of motion. In this process the JointsMethod only does the “book-keeping” of the joints. It uses another method, like the KanesMethod, as its backend for forming the equations of motion.

In the code below we form the equations of motion of the single PrismaticJoint above.

>>> method = JointsMethod(parent, joint)
>>> method.form_eoms()
Matrix([[-child_mass*u1']])
>>> type(method.method)  # The method working in the backend
<class 'sympy.physics.mechanics.kane.KanesMethod'>